Zero Knowledge Proofs: Empowering the Future of Data Privacy and Scalable Infrastructure

Exploring Zero-Knowledge Proofs (ZKPs), use cases and their potential in improving our digital lives.

Feb 29, 2024

Zero-Knowledge (ZK) technology is a big deal in the world of Web3, but it can be a bit tricky to understand at first. So, we're going to split this article into two parts. The first part provides a high-level introduction to what this technology is and why it's so important, including its general use cases.
Before you dive into the second part, it's a great idea to check out the video linked at the end of the first part. It features a computer science expert breaking down Zero-Knowledge Proofs across various levels of complexity. This will help you get a solid grasp of the basics of ZK technology.
In the second part, we will dive deeper into how ZKPs are changing the game in the blockchain domain, spotlighting major projects that tackle big issues like making things faster & more private. Plus, we'll prepare you to explore further on your own by clarifying some common terminology that you might come across in ZK research papers.

Part 1 - Fundamentals of Zero Knowledge Proofs

A Zero-Knowledge Proof (ZKP) enables one to prove the knowledge or truth of a statement without revealing the information itself. It's like being able to prove you know a secret password without having to tell anyone what the password is. This method is really important in keeping information safe and private while still showing that you're telling the truth.

Zero Knowledge Proofs (ZKPs) offer a revolutionary approach to enhancing privacy and security across various domains. In privacy-preserving authentication, ZKPs allow individuals to prove their identity without disclosing sensitive information, effectively minimizing the risk of data breaches. In the realm of blockchain and cryptocurrencies, they enable transactions that are both private and verifiable, addressing the critical need for confidentiality without compromising on transparency. Furthermore, in secure voting systems, ZKPs ensure the integrity of the electoral process by allowing votes to be counted without revealing the voters' identities, thus upholding the principles of anonymity and fairness.

The two parties involved in a ZKP are:

Prover: A prover is someone who tries to prove they know a secret without actually showing the secret.
Verifier: A verifier is someone who checks the proof given by the prover to see if their claim is true, without learning the secret. The verifier can believe the claim is true by looking at certain details of the proof.

In a Zero Knowledge Proof (ZKP), the prover aims to demonstrate their knowledge of a secret without revealing the secret itself, while the verifier assesses the proof's validity, ensuring the claim is true without gaining any knowledge of the secret based on specific details of the proof provided.

Why should we care about zero-knowledge-proof technology?

Zero-knowledge-proof technology could be really useful in many different areas, considering how important it is to keep things private and secure online. ZKP could help people and businesses interact safely, making sure private information stays private, which is super important in places like banks, hospitals, and even when voting. Here are some key use cases and reasons why you should care about ZKPs:

Supply Chain Integrity: Zero-knowledge proofs in supply chains are like a seal of approval that proves a product is genuine and comes from where it says it does, without giving away trade secrets. For example, a chocolate company can prove their cocoa comes from ethical sources without revealing their suppliers or how much they pay them. This keeps the supply chain transparent, ensuring products are safe and authentic, which is super important for things like medicines and designer bags, helping consumers trust what they buy.
Privacy-preserving Authentication: Using zero-knowledge proof technology for privacy-preserving authentication is like showing your ID to prove your age without having to reveal your birthdate or any other private info. It lets you prove who you are online without revealing sensitive information. This makes the internet safer for everyone by lowering the chances of personal information getting stolen.
Blockchain and Cryptocurrencies: Zero-knowledge proofs in blockchain let people do transactions without showing how much money is being moved or who is involved. But, everyone can still be sure the transaction is real and follows the rules. This is great for keeping financial activities private and secure, making it more attractive for both regular people and big companies to use without worrying about their transaction details being exposed.
Secure Voting Systems: Zero-knowledge proofs in voting are like secret ballots that let you check your vote was counted without showing who you voted for. This keeps voting private but makes sure every vote is right, helping keep elections fair and honest. It's like voting in a booth where you can make sure your vote is in the box without anyone else seeing who you picked.
Confidential Compliance: Zero-knowledge proofs enable companies to demonstrate they've complied with tax laws without revealing detailed financial information. Imagine a business being able to confirm it has paid all necessary taxes correctly, without having to disclose its total earnings or specific business strategies. This method protects the company's private financial details while still assuring the authorities of its compliance

In essence, Zero-knowledge proofs (ZKPs) are a groundbreaking technology that safeguards privacy and security in digital interactions, from online authentication to blockchain transactions and voting systems. They enable one party to prove the truth of a statement without revealing any information beyond the statement's validity. This capability is crucial for maintaining privacy, securing online transactions, and ensuring the integrity of digital processes, making ZKPs an essential tool for building trust in our increasingly digital world.

Please check out this engaging video featuring a computer scientist expert explaining Zero-Knowledge Proofs across various levels of complexity.

Call for Zero-Knowledge Startups and Experts: We're looking to engage with startups and experts in the zero-knowledge (ZK) technology domain. If you're innovating in the ZK field, we invite you to connect with us. We're committed to a future where online privacy and trust are paramount. If you're eager to make a difference, we'd love to hear from you. Please feel free to either connect on LinkedIn or contact us at pitch@blockwall.capital.

Part 2 - Deep Dive into Zero-Knowledge Proofs(ZKPs)

In this part, we will dive further into the use case of ZK within the blockchain domain, and discuss major projects that are addressing the most pressing challenges in the blockchain ecosystem. Plus, we'll explore some of the common terminology you might come across in ZK research papers.

Let’s have a look at the different use cases and which blockchain startups are actively addressing these use cases:

Privacy: ZKPs can be used to enhance privacy, for example, in blockchain transactions, by concealing the transaction details, sender, recipient, and transaction amounts while still ensuring the transaction's validity. Some projects focusing on this use case are Zcash, Monero, Tornado Cash, and Mina.
Scalability: By bundling many transactions together, doing calculations off the main network, and using zero-knowledge proofs, ZK rollups help make the blockchain faster and less crowded. This method makes transactions quicker and cheaper, while still keeping them secure. It means more transactions can happen smoothly and affordably, helping more people use blockchain technology. One of the projects focusing on this use case is Starkware.
Interoperability: ZKPs can make it safe and privacy-preserving for different blockchain networks to work together, allowing assets or data to move smoothly between them. With ZKPs, details about these assets or data stay secret, making sure that privacy is protected during the transfer process. Projects like zkBridge, Electron Labs, and Polymer Labs are working on this.
Identity: Using zero-knowledge proofs (ZKPs), people can confirm who they are or that they belong to a network without showing any private or identifying details. This lowers the chance of identity theft or someone getting unauthorized access. ZK-DID is a project focusing on this.

As discussed above Zero-Knowledge Proofs (ZKPs) have various applications in the field of blockchain technology. Let’s further explore the ZKPs use cases:

ZK-rollups: A rollup is a layer-2 scaling solution that offers a way to make blockchain transactions faster by handling them off the main chain, which is called layer-1. A rollup removes transactions from the mainnet for off-chain processing. These transactions are then consolidated into a single data entity and then resubmitted onto the parent chain. By shifting intensive computations off-chain, significant efficiency gains are achieved. ZK-rollups use something called validity proofs. These are special codes that prove a group of transactions or a calculation was done right in the ZK-rollup. Then, a special program on the main chain checks this code to ensure every transaction is done correctly.
zkEVMs(EVM-compatible zk-Rollup): zkEVM lets smart contracts, usually written in high-level languages like Solidity, be used in a zero-knowledge proof environment. First, a compiler turns the Solidity code into bytecode. The Ethereum network then runs this bytecode with the help of the Ethereum Virtual Machine (EVM). A zkEVM is a special EVM that can handle these tasks and use zero-knowledge proofs, making it possible to do things privately and efficiently. Here is a post from Vitalik where he classifies zkEVMs into four categories.

ZK bridges: Cross-chain bridges are currently facing security and scalability issues. In the case of cross-chain bridging, an on-chain light client could be used to verify the state of the source blockchain on the target blockchain. A ZK-bridge utilizes Zero Knowledge Proofs to efficiently perform this verification process using on-chain light clients. ZK bridges could play a significant role in enabling seamless interoperability and secure asset transfers across different blockchains.
Client-side ZK: It refers to the use of zero-knowledge proofs (ZKPs) directly on the user's device or client-side application rather than relying on centralized servers. This approach allows users to generate and verify proofs about their data or actions without revealing sensitive information to third parties. Client-side ZK is often employed to enhance privacy and security in various applications such as identity verification, compliance with regulations like KYC (Know Your Customer) and AML (Anti-Money Laundering), and decentralized advertising platforms. Projects like Zk.me and Brave Boomerang are working on this.

Types of Zero-Knowledge Proofs

The most commonly used ZKPs are zk-SNARKs, zk-STARKs and Bulletproofs.

zk-SNARK stands for Zero-Knowledge Succinct Non-interactive Argument of Knowledge. This means the proofs are small and easy to check. Initially, zk-SNARK needed a trusted setup, but thanks to advances in zero-knowledge research and projects like Spartan, we can now have zk-SNARKs without needing a trusted setup.
zk-STARK stands for Zero-Knowledge Scalable Transparent Argument of Knowledge. zk-STARKs can confirm that calculations done off the blockchain are correct without showing the data used. zk-STARKs are seen as better than zk-SNARKs because they can handle more data and are more open. The best part about zk-STARKs is that they don't need a trusted setup. The "Transparent" in their name means they use randomness that everyone can see to create their parameters, so there's no need for a trusted setup anymore.
Bulletproofs are a type of zero-knowledge proof that is short and doesn't need to interact with others. They don't require a trusted setup either. While Bulletproofs are compact, they aren't as cost-effective as validity rollups. Currently, Monero uses Bulletproofs.

Major projects in the Zero-Knowledge Proofs landscape

Starkware: Founded in 2018, the vision of StarkWare is to bring scalability and privacy to blockchains with zero-knowledge STARK proofs. They have two main offerings (a) StarkNet is a permissionless decentralized validity rollup and (b) StarkEx is a SaaS version tailored to be used by protocols e.g. dYdX v3 was using StarkEx.

zkSync: Matter Labs, founded in 2020, started the zkSync project. It's a Layer 2 solution that makes Ethereum faster using zero-knowledge proofs (ZKPs). They later launched zkSync 2.0, now called zkSync Era. This new version introduced zkPorter, a feature that uses advanced ZKPs to bundle many transactions into one proof. This greatly improves how much zkSync can handle, making Ethereum more scalable.

Scroll: They are building a Type 2 zkEVM, a native zkEVM solution for Ethereum i.e. no compiler is needed. A Type 2 zkEVM is fully equivalent to the EVM. It differs from Ethereum in terms of block structure and state tree. In an EVM-equivalent environment, most of the Ethereum toolchain could be used without much difficulty. Scroll is also closely working with the Ethereum Foundation’s Privacy and Scaling Explorations (PSE) group(also working on a ZK-EVM).

Polygon zkEVM: In 2021, Polygon bought Hermez for $250 million, and it was later renamed Polygon zkEVM. Their zkEVM uses a special interpreter to change EVM opcodes (the basic instructions Ethereum uses) into zkASM, which is Polygon's own assembly language. Polygon's method turns each EVM opcode into a zkASM opcode, and then back into EVM bytecode. Polygon says their zkEVM works perfectly with the tools already used for Ethereum

Common terminology that appears in the ZK research papers

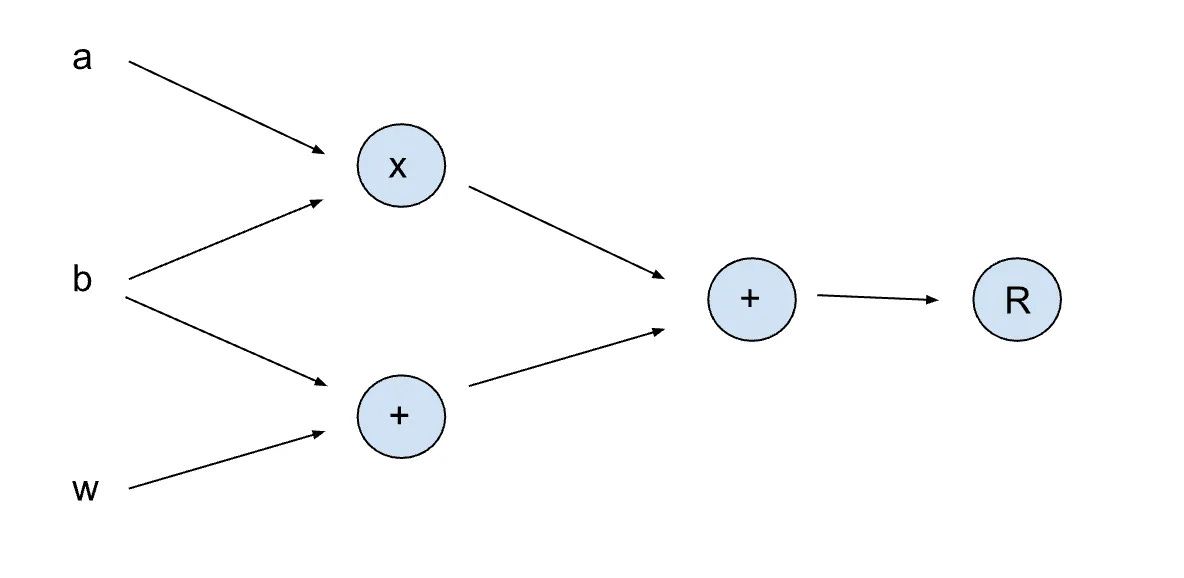
Arithmetic Circuit: To create a zero-knowledge proof (ZKP) for a problem using zkSNARKs, the first step is to simplify it into a basic math form using simple arithmetic operations. Most zkSNARKs work with problems called circuit satisfiability. Here's the math circuit for the equation (a*b) + (b+w) = R

Boolean Hypercube: It represents all possible combinations of boolean values for n dimensions e.g. the boolean hypercube for the set {0,1}³ will be {000, 001, 010, 011, 100, 101, 110, 111}.
Elliptic Curve Cryptography: It is a cryptographic method that leverages the properties of elliptic curves to secure our digital information, such as private messages, sensitive data, or online transactions.
Fiat-Shamir Transformation: This technique in cryptography changes a proof system that needs interaction into one that doesn't require any interaction. The "interaction" refers to the communication between two parties, the prover and the verifier.
Finite Field: In a finite field, the number of elements is limited. A binary field is a finite field where the elements can only be either 0 or 1. This means that addition, subtraction, multiplication, and division operations within the binary field will result in either 0 or 1.
Folding Scheme: The folding scheme reduces the size of the data by folding each block into a smaller value while preserving certain properties. Let’s understand Folding using the modulo operation example: Suppose we have a message consisting of a sequence of digits 981526937, after partitioning into 5 parts i.e. 98,15,26,93,7 and folding operation using modulo 10 e.g. for 98, 9+8=17, modulo 10 will result in first digit 7. The compressed representation of 981526937 will be 76827.
GKR Protocol: GKR (Garg, Kalai, and Raz) protocol is used as a building block to perform efficient polynomial evaluations. It enables the prover to convince the verifier of the correctness of polynomial evaluations without revealing the polynomials themselves.
Hash Function: A hash function is a mathematical function that takes an input and produces a hash value, which is unique to the input data. e.g. The SHA-256 hash value for “Hello World” is: b94d27b9934d3e08a52e52d7da7dabfac484efe37a5380ee9088f7ace2efcde9
Interactive Proofs: In an interactive proof system, the prover and verifier engage in multiple rounds of communication. The prover sends information (challenges) to the verifier, and the verifier checks the responses to determine the validity of the statement.
NP class problems: The NP class refers to a class of computational problems that can be verified in polynomial time.
Non-interactive proof: With the Fiat-Shamir transformation, the prover can generate a non-interactive proof by computing the responses to the challenges without any further communication. The verifier can independently compute the same challenges using the hash function and compare the responses provided by the prover to validate the proof.
Opcodes: Operational Codes (Opcodes) represent the individual instructions that the EVM can execute. Each opcode corresponds to a specific operation, such as arithmetic, logical operations, memory access, or control flow. Here is the full list of Ethereum Opcodes.
PLONK: PLONK (Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge) is a new general-purpose zero-knowledge proof scheme. Here is the article Vitalik wrote on PLONK.
Polynomial time: Polynomial-time means that the time it takes to solve a problem grows at a reasonable rate as the problem gets bigger. It’s like having an algorithm that can handle larger and more complex tasks without taking too much time to find a solution.
Polynomial Commitment Scheme: The Polynomial Commitment Scheme lets us make commitments to the results of a polynomial at certain points without showing the coefficients of the polynomial. Others can check these results by recalculating the commitments with the shared commitment and result values. This way, they can confirm the results are correct without knowing the specifics of the polynomial.
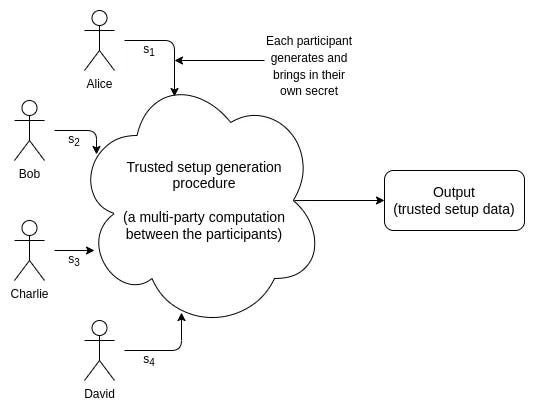
Powers of Tau: In the trusted setup phase, a group of participants collaboratively performs a multi-party computation protocol. Each participant contributes a random value known as a “contribution” and applies a series of cryptographic operations to derive a combined “toxic waste” value. The resulting toxic waste value is transformed into a set of public parameters, known as the Powers of Tau.
R1CS: R1CS stands for “Rank-1 Constraint System,” which is a mathematical representation of a computational problem.
Random Oracle: It is a function that takes any input and produces an unpredictable and unique output.
Sum Check Protocol: The Sum Check Protocol is a technique used in interactive proof systems to efficiently verify the sum of values computed by a prover without revealing the individual values themselves. It allows a verifier to interact with a prover to determine if the sum of certain values meets a specific criterion.
Simulation Paradigm: A simulation paradigm is an approach used in cryptography to analyze the security of cryptographic protocols. It involves designing protocols such that the behavior of adversaries can be effectively simulated, allowing for the evaluation of security properties without the direct participation of the adversaries themselves.
Trusted Setup: In the trusted setup phase, a group of participants collaboratively performs a multi-party computation protocol. Each participant contributes a random value known as a “contribution” and applies a series of cryptographic operations to derive a combined “toxic waste” value.

Validity Proof: A validity proof refers to a cryptographic proof that demonstrates the validity of a batch of transactions or a computation within a ZK-rollup construction.
Witness: In the context of NP class problems, a witness is a solution or piece of evidence that demonstrates the truth of a statement.

Summary

The exploration of the Zero Knowledge Proofs (ZKPs) landscape reveals the transformative potential of ZKPs in enhancing blockchain technology through privacy, scalability, and interoperability. ZKPs enable a secure method of proving the validity of transactions or statements without revealing any underlying data, thereby ensuring user privacy and data security. The introduction of ZK-rollups, zkEVMs, and ZK-bridges underscores the versatility and efficiency that ZKPs bring to the blockchain, offering solutions to longstanding issues like network congestion and high transaction costs. Projects such as Zcash, Monero, Mina, and Starkware are at the forefront, driving innovation within the ZKP landscape.

References:

Disclaimer

To avoid any misinterpretation, nothing in this blog should be considered as an offer to sell or a solicitation of interest to purchase any securities advised by Blockwall, its affiliates or its representatives. Under no circumstances should anything herein be interpreted as fund marketing materials for prospective investors considering an investment in any Blockwall fund. None of the data and information constitutes general or personalized investment advice and only represents the personal opinion of the author. The author and/or Blockwall may directly or indirectly be exposed to the mentioned assets/investments. For further information please view the full Disclaimer by clicking the button below.

Disclaimer

This work is licensed under the Creative Commons Attribution – No Derivatives 4.0 International License. CC BY-ND 4.0 Legal Code | Creative Commons

Blockwall Insights

Discussion about this post